Activation Function
: cell body의 linear 성분을 non-linearity로 변경해주는 역할

Sigmoid

: 전통적으로 많이 사용했지만, 지금은 잘 사용되지 않음.
: 넓은 범위의 수를 0~1로 squash해줌.
Problem
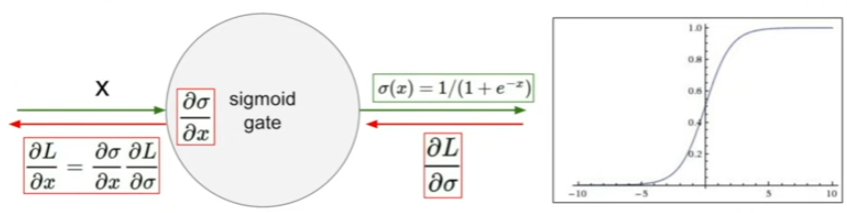
1. vanishing gradient : neurons이 staturated 되어, gradients를 죽이는 것
: backpropagation에서 chain rule을 사용해서, gradient를 구하는데,
x값이 크거나 작을 경우, 미분값이 0이므로 곱해지는 미분값이 0이 되기 떄문에
그 후 gradient들에 대해서 다 0이된다. 즉 gradient가 kill, 이때, 미분값이 0에 수렴되는 x축 범위를 포화지점, staturated regime이라고 부름
2. not zero-centered
: sigmoid의 중앙값이 0이 아니다.
: input neurons이 언제나 양수라고 가정했을 떄, w(gradient)는 어떻게 될까?
sigmoid의 미분값음 항상 0이상의 값이다. 그렇기 때문에 backpropagation단에서 모든 weight의 부호가 동일해진다.
이때, 2개의 weight(w1,w2)가 있으며 w1은 작게, w2는 크게 설정하는 것이 optimal이라고 한다면,
w1은 음, w2는 양으로 update하는 것이 불가능하다는 것이다.
따라서, sigmoid를 통해 이를 update하려면, w1은 작게 + w2는 크게 +, 그 다음 스텝은 w1은 크게 -, w2는 작게 - 하는 형식으로 update해야된다.
이 문제로 인하여 수렴에 있어서 zig zag path로 수렴점에 도달하기에 수렴 속도가 느려진다.
(추가적으로, batch norm, data regularization이 도움이 되는 이유도 이에 있다.)

3. sigmoid에서 exp()는 compute expensive하다.
Tanh

: sigmoid와 비교했을 때, 범위가 0~1이 아닌 -1~1로 확장 및 zero-centered
: 이로써, sigmoid의 문제를 완벽히 해결하진 못함 (vinishing gradient)
ReLU

: 현재 많이 쓰이는 activation function
: 양수에 대해 staturate, compute가 efficient하여 sigmoid/tanh에 비해 매우 빠름
Problem
1. not zero-centered
2. Dying ReLU
: x가 만약 -10일 떄? 기울기는 0 -> 음수에 대해 gradient가 죽어버리는 현상
: x가 0일 때 미분 불가능점이라 gradeint undefined
: weight 초기화시나 learning rate가 높게할 경우 dead ReLU존으로 갈 수 있겠다.
: 이를 방지하기 위해 bias를 작은 positive값으로 초기화하는 등이 있음.

Leaky ReLU

: negative value에 대해 아주 작은 값을 줌으로써 미분이 0이 아니도록
: (0.01대신, alpha값을 넣, PReLU도 있음 여기서 alpha는 parameter)
: PReLU에 비해 Learky ReLU는 음수값에 대해 0.01이라는 고정된 gradient를 가지고 있어서 최적의 성능은 아닐 것 같다.
ELU

: exp()를 사용해서 compute expenssive
: ReLU 변환 형태들은 negative에서의 문제를 해결하기 위해 여러 가지 방법 존재
: ReLU의 장점을 다 가지지만, 연산이 너무 많음...
Maxout

: not saturate, not die ( 음수에 대해서도 정의되고, 양수에 대해서도 정의된다.)
: 단점으로는, Neuron 하나에 대해 k개의 feature가 필요로 하기에 연산량 k배 증가
: dropout으로 선택을 하게 함으로써 maxout + dropout 합친 형태를 주로 본 것 같다.

Data Processing

: image라고 생각해보면, zero-centered는 일반적으로 해줄 필요가 있지만, normalizaed는 특정 범위 내에 들어가도록 하는 것인데, image자체가 0~255라는 범위가 있기에 굳이 해줄 필요는 없을 것이다.

: 2번째와 같은 PCA는 data의 차원을 줄여주고, 데이터를 잘 표현할 수 있도록 Projection 찾기
: whiening은 data들을 uncorrelated하게 만들고, variance를 1로 만드는 것
Weight Initalization
: 여기서는 강의에서 다룬 내용이 아닌 다른 내용으로 설명
Lecun
: Uniform distribution, Nin은 input neuron의 수
: 해당 범위 사이에서 랜덤하게 값을 뽑는다.
: 아래의 수식은 왼족과 오른쪽 평균,분산은 동일
: 0근처 값에서 랜덤하게 잡을건데, 랜덤하게 잡을 범위를 제한

Kaiming
: ReLU를 사용하는 신경망에서 위보다 자주 쓰이는 것 같음
: Lecun에서 분산 2배 방식

Xavier
: 분산이 kaming보다는 작아서 sigmoid/ tanh 사용하는 신경망에서 kaming에 비해 자주 쓰일 것 같음
sigmoid, tanh의 vanishing gradient 문제때문에

이런식으로 weight initalization을 하지 않고, 0 or 1로 weight를 initalization하면?
0으로 다 초기화해버리면 그 이후 neurons들에 대해 update를 안할 것이고,
1로 다 초기화를 해버리면 같은 layer neurons은 동일한 output을 생성할 것이다. (즉, weight를 동일하게 update하며, neurons은 서로 다른 feature를 학습하지 못할 것)
Batch Normalization
: vanishing gradient problem을 없애기 위한 방법
: mini batch 단위로 normalization하자.
: 수식을 통해 output값을 activation function에 넣기 전 normalization
: batch 단위의 output 값들을 재배치 시킬지 학습



'Study > cs251n' 카테고리의 다른 글
| CS231n : lecture11,13_CNNs in practice, Segmentaiton (0) | 2024.12.10 |
|---|---|
| CS231n : lecture10_Recurrent Neural Networks, Image Captioning, LSTM (1) | 2024.12.09 |
| CS231n : lecture5_Convolutional Neural Networks (0) | 2024.12.07 |
| CS231n : lecture4_Introduction to Neural Networks (0) | 2024.12.04 |
| CS231n : lecture3_Loss Fn, Optimization (0) | 2024.12.04 |
