Backpropagation
forward pass에서 local gradient를 구하고
backward pass에서 global gradient를 구한다.(local gradient를 chain rule을 활용해서)
: chain rule을 통해 local gradient와 global gradient의 곱으로써 표현해서 계산
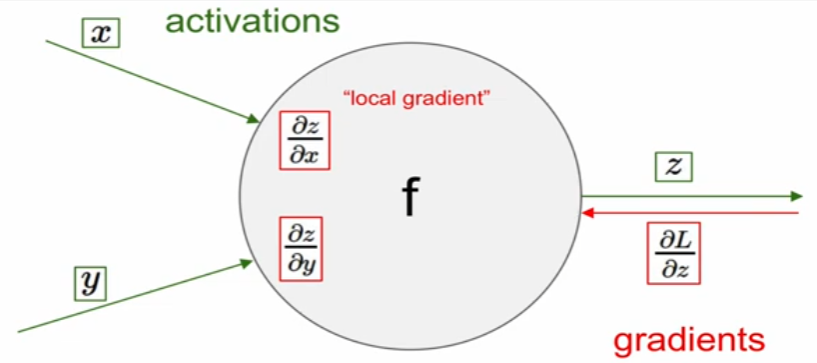
아래에 예시에서 살펴보자면
: add gate -> gradient distributor, 전의 gradient를 그대로 전파
(local gradient의 값이 1이므로)
: max gate : gradient router
: mul gate : gradient switcher, local gradient가 바뀌기 때문에
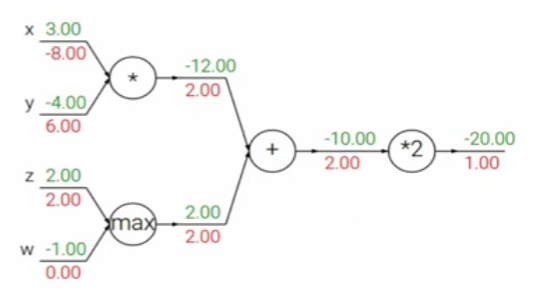
즉, 위를 정리해보자면
local gradient
1. local gradient는 foward pass 때 구할 수 있다.
2. local gradient를 구해서 메모리에 저장해둔다.
global gradient
1. backward pass 때 구할 수 있다.
2. 메모리에 저장한 local gradient와 곱해서 gradient를 구한다.
3. backward pass때, chain rule이 일어난다.
Neural Network
: 이전 linear score function은 f = Wx
: 2-layer Neural Network일 경우 f = W_2 * max(0,W_1*x)
-> 기본적으로 max는 ReLU를 뜻한거 같다. ReLU는 activation function 중 하나.
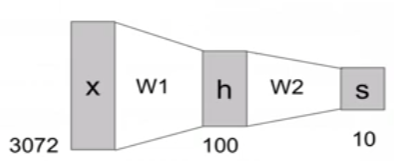
: 그럼, data-drive approach와의 차이를 보면?
-> 이미지에서 다양한 색상, 형태 등이 있는 이를 합쳐서 표현했었다. (한계)
-> 즉, 하나의 class에 대해 하나의 classfier만 존재
-> Neural Network는 이를 node로 각각의 feature들을 표현가능
-> 즉, 하나의 class에 대해 여러 개의 classfier가 존재
activation function을 적용해서 non-linearlity하게 하여 output 하는데,
전통적으로 sigmoid activation function을 보면,
y값은 0 ~ 1로 표현할 수 있기에 확률을 0~1로 특정지을 수 있어서 많이 사용했었다.
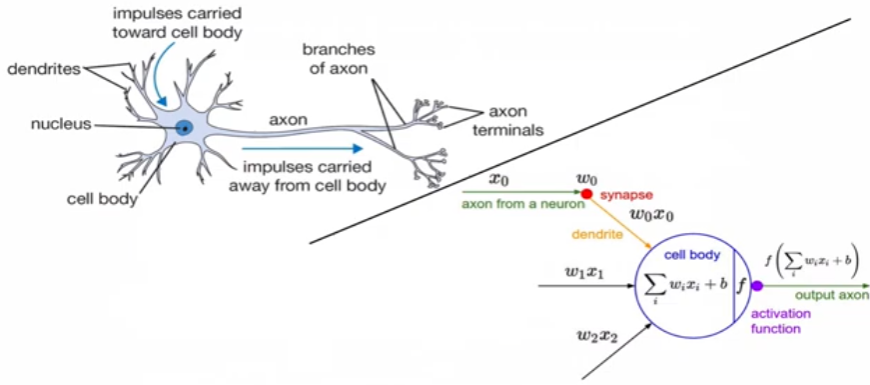
Activation Function
: 2017년 강의기에 GELU 등장 이전 강의인가?
: 아래의 문제점들을 각각 찾아보며 다른 activation function들을 소개하도록 하겠다.
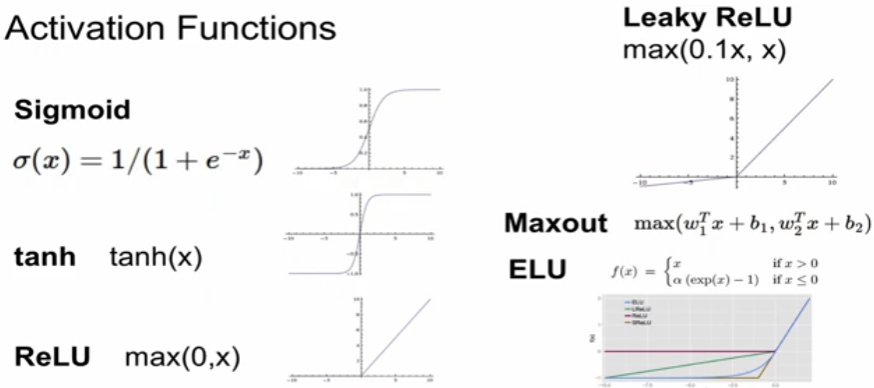
Activation Problem 1. Gradient Vanishing
1. Sigmoid Function
: 범위를 0~1로 제한함으로써 쉽게 확률적으로 표현 가능하다.
sigmoid function의 미분값부터 살펴보자.
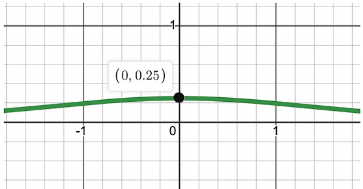
: sigmoid의 미분값을 보면, y값이 0과 1에 수렴할 때, 0에 가까워지는 것을 확인할 수 있다.
: 추가적으로 0일 때도 0.25 밖에 되지 않는다.
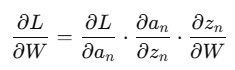
: 여기서, 각 layer의 gradient는 이전 layer의 gradient와 activation function의 미분값에 의해 감소 또는 증가한다.
: 따라서, backpropagation 과정에서 미분값이 계속 곱해진다면, 출력 layer와 멀어질 수록 gradient값이 매우 작아질 수 밖에 없다.
2. Tanh
: sigmoid의 확장형으로 -1~1 범위로 확장
: tanh의 경우 sigmoid보다 범위를 2배 확장했다고 볼 수 있다.
: 추가적으로, 미분값을 보면 sigmoid의 비해 훨씬 커졌다.
: 하지만, tanh 역시 x값이 0기준으로 증가또는 작아짐에 따라 기울기가 크게 작아진다.
: 따라서, 기울기 소실 문제를 완벽하게 해결하지는 못했다.
3. ReLU
gradient vanishing problem을 해결하기 위해 ReLU가 등장했다.
: max(0, x)의 형태로써 양/음수로 나누고 양의 값은 x, 음의 값은 0인 형태. 미분값이 0또는 1이다.
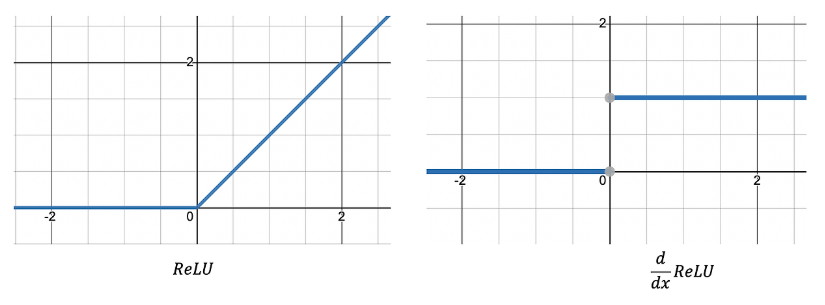
Activation Problem 2. Dying ReLU
: 앞서 본 ReLU의 경우 음수이면 미분값이 0이다. 따라서 입력값이 음수인 뉴런에 대해 회생시키기가 어렵다.
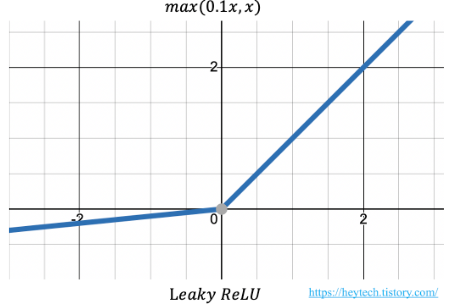
: 이를 해결하기 위해 Leaky ReLU가 등장한다.
4. Leaky ReLU
: 음수값에 대해 0으로 표현되는 ReLU와 달리 a*x로 표현 (0<a<1)
: 다음으로 입력값이 음수인 경우에 미분값이 0이 되지않아 뉴런이 죽는 현상을 방지
이후 추가적으로, PReLU, ELU, Swish, GELU등이 등장한다.
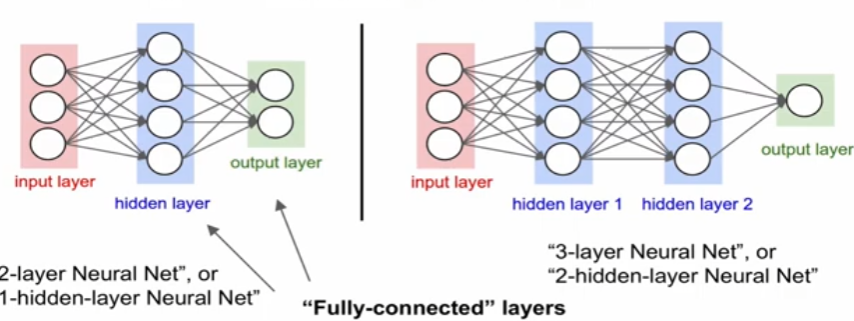
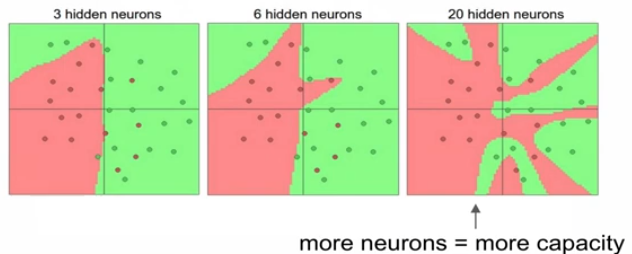
Neural Networks Architecture
: 일반적으로, layer가 많을 수록 feature를 계산, 학습하는 weight가 많아지므로 capacity가 높아진다.
: 추가적으로 data의 overfitting되지않도록 layer자체를 줄이는 것 보다 regularization을 잘 설정해야된다.
'Study > cs251n' 카테고리의 다른 글
| CS231n : lecture10_Recurrent Neural Networks, Image Captioning, LSTM (1) | 2024.12.09 |
|---|---|
| CS231n : lecture6,7_Training Neaural Networks (0) | 2024.12.09 |
| CS231n : lecture5_Convolutional Neural Networks (0) | 2024.12.07 |
| CS231n : lecture3_Loss Fn, Optimization (0) | 2024.12.04 |
| CS231n : lecture2_Image Classification pipline (1) | 2024.12.04 |
