Image Classification : a core task in Computer Vision
(assume give set of discrete labels) : {dog, cat, truck, plane, ...} -> cat !

Problem : semantic gap
: image는 기본적으로 숫자로 구성된 3d array (0~255의 color 숫자, 3d channel)

Challenges 1 : Viewpoint Variation
: viewpoint가 다름에 따라 image를 다르게 보일 수 있는 문제

Challenges 2 : Illumination
: 조명에 따라 이미지의 색상 정보가 바뀌는 문제.

Challenges 3 : Deformation
: 형태의 변형 문제

Challenges 4 : Occlusion
: 폐색 (가려짐 등) 문제

Chanllenge 5 : Background Clutter
: 배경과의 색상이 비슷한 문제

Chanllenge 6 : Intraclass variation
: 같은 class 내에서도 다양성(분산)에 대한 문제

해당 문제들에 대해 Image를 input 받아서 class를 output 하는, 즉, image에 대해 인식하는 것은
하드 코딩할 수 있는 명백한 algorithm이 존재하지 않음
역사적으로 어떤 시도를 했을까?
: image에 대해 edge detection(or shape 등의 feature를 추출하는 방법)을 시도하고,
image의 상태를 비교해서 탐색하는 방법
: 아래의 사진을 보면, edge를 통해 오른쪽의 특징이 있으면, 어떤 class인가? 를 탐색하는 방식
: scalable problem
: 잠깐, 생각해봤을 때도 pre-knowledge로 특정 class마다 pattern을 구조화 시켜놔야된다는 것 자체가 문제가 크게 될 것이다.

해당 문제를 해결하기 위한 방법은?
Data-driven Approach
1. images와 labels의 dataset을 모으고,
2. image classifier를 학습하여
3. test image dataset에 대해 평가를 실시
: 따라서 훈련 및 예측으로 분할

First classifier : Nearest Neiighbor Classifier
: CIFAT10 dataset 사용
: 10class, 5만개의 training image, 1만개의 test image로 구성 (32x32x3 pixel small image)

: 우선, 결론을 먼저 보자면, 아래의 사진이다.
: 예를 들에 가장 왼쪽 위 이미지에 대해서는 첫번째부터 열 번째 가깝다고(비슷하다고) 생각하는 이미지를
오른쪽에 보인다.

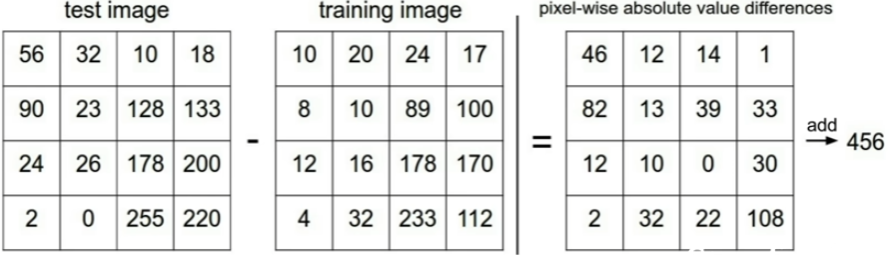
: L1 distance 사용 (Manhatann distance) :
: 두 image에 대해 element-wise difference를 구하고 sum하는 형태
: 아래의 코드로 간단하게 테스트 가능하며, 실제로는 x_train에 image data, y_train에 해당 image들의 labels,
x_test에 test image를 삽입하면 위의 image와 같은 결과를 볼 수 있다.

import numpy as np
class NearestNeighbor :
def __init__(self) : pass
def train(self,x,y) :
"x is image, Y is label"
# x,y를 assign 해줌으로써 memory에 올리기
self.xtr = x
self.ytr = y
def predict(self,x) :
image_num = x.shape[0]
y_pred = np.zeros(image_num, dtype=self.ytr.dtype)
for i in range(image_num) :
distances = np.sum(np.abs(self.xtr - x[i, :]), axis=1) # 각 샘플과의 L1 거리 계산
y_pred[i] = self.ytr[np.argmin(distances)]
return y_pred
# Sample data
x_train = np.array([[1, 2], [3, 4], [5, 6]])
y_train = np.array([0, 1, 2])
x_test = np.array([[1, 2], [4, 5]])
# Initialize and train
nn = NearestNeighbor()
nn.train(x_train, y_train)
# Predict
y_pred = nn.predict(x_test)
print(y_pred) # [1,2] is label 0, [4,5] is label 1or2 -> argmin이니 index가 작은 1k-Nearest Neighbor (KNN)
: k개의 nearest images를 찾고, label을 선택(투표)
: 위의 10개의 image 결과를 낸 것이 k=10인 10-NN이라고 볼 수 있다.

Distance Metric
: 앞서는 L1 distance 맨허튼 거리를 사용했는데, L2 distance인 유클리드 거리를 보면 아래의 사진과 같다.
: distance metrice을 바꿈에 따라 당연히, 경계에 있는 class 선택에 대해서는 다른 결과를 보일 것이다.

Hyperparameters
: 위의 distance metric만 보더라도 문제에 따라 선택을 해야되기에 hyperparameter라고 볼 수 있다.
: k-NN을 보면, K 또한 hyperparameter라고 볼 수 있다.
: 그럼, 우리는 hyperparameter를 어떤 식으로 수정해야될까?
: 전제 ) test dataset은 최종 성능 평가에 대해 최후의 보류로 남겨놓아야 된다.
: train dataset에서 분할하여 validation dataset을 확보

: 하지만, train dataset이 충분하지 않아서 분할할 정도의 양이 없다면?
: train dataset에서 일부분으로 나누고, cross-validation 수행
: 아래는 k-fold validation (k=5)

: k-NN에 대해서 적용해보면
: k-fold validation (k=5) 에 대해 k=7일 때, validation에 대해 정확도의 평균 (validation 1개에 대한 4개의 fold의 정확도 평균)이 가장 높은 것으로 보이므로 k=7 7-NN을 수행하는 것이 해당 문제에서는 가장 적합

하지만, 당연하게도 K-NN method는 distance 기반으로 찾는 것이기에... 현실에는 적용하지 힘들다.
예시로써, 아래의 original image에 대해 오른쪽 3개의 image는 L2 distance가 같다.

Linear Classification
: dataset은 앞의 CIFAR-10 사용
: 앞의 방법과 달리 parameter (Weight) 사용
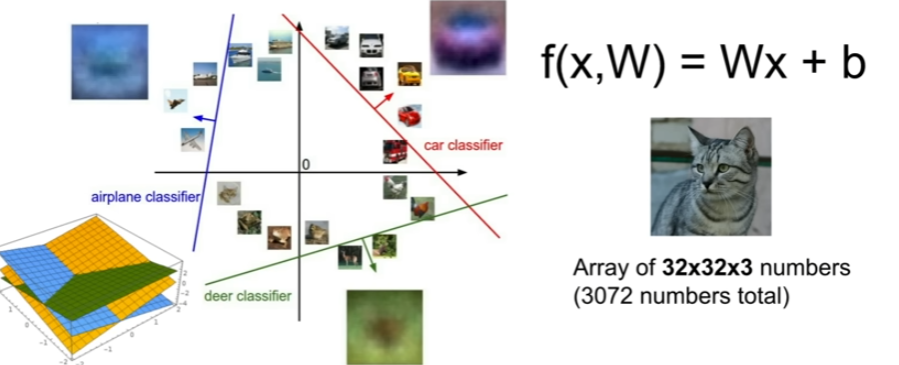
: f(x, W) = Wx + b
example. 32x32x3 image를 10classes 중 예측하려면?
: 10x1 = W conv (3072x1) + b
: 10x1 = 10x3072 conv (3072x1) + (10x1)이다.
: 즉, 학습되는 weight는 10x3072의 크기이며, bias는 10x1
: 아래의 사진과 같은 4pixel의 고양이 이미지를 예측
: 이 때, wegiht 및 bias가 학습되면서 cat score가 높도록 조정

: CIFAR-10 dataset에 대해 train된 weight를 보면 아래와 같다.
: 자동차를 보면, 빨간색 차가 데이터셋에 많아서 빨간색으로 형성
: 결론적으로, 노랑색 차는 frog로 판별할 가능성이 높음
: 즉, 색상에 많은 영향을 받는 문제, capacity의 한계

: 다음과 같이 class를 영역으로써 분할한다.
3강에서는
1. loss function
2. optimization
3. convNet에 대해 학습한다.
'Study > cs251n' 카테고리의 다른 글
| CS231n : lecture10_Recurrent Neural Networks, Image Captioning, LSTM (1) | 2024.12.09 |
|---|---|
| CS231n : lecture6,7_Training Neaural Networks (0) | 2024.12.09 |
| CS231n : lecture5_Convolutional Neural Networks (0) | 2024.12.07 |
| CS231n : lecture4_Introduction to Neural Networks (0) | 2024.12.04 |
| CS231n : lecture3_Loss Fn, Optimization (0) | 2024.12.04 |
