Chapter 8에서는
* 제곱근 변환의 사용 시기 및 탐색 방법을 식별하는 방법
* 로그 변환의 사용 시기 및 탐색 방법 및 원시 데이터에 대한 기대 사항
* Box-Cox 변환을 사용하여 제곱근, 로그 작업을 수행하고 dataset에 가장 적합한 변환을 자동으로 찾는 방법
* 에 대해 배운다.
Airline Passengers Dataset
* Airline Passengers dataset은 시간 경과에 따른 총 항공사 승객 수에 대한 Time Series이다.
# load and plot a time series
from pandas import read_csv
from matplotlib import pyplot
series = read_csv('airline-passengers.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(series)
# histogram
pyplot.subplot(212)
pyplot.hist(series)
pyplot.show()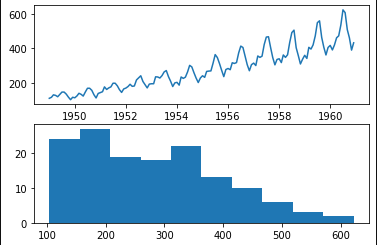
Square Root Transform
* 2차 곡선 trend를 가지는 Time Series는 제곱급을 사용하여 선형으로 만들 수 있다.
* 아래는 1~100까지의 수를 만들고 이를 제곱하여 시각화한 예제이다.
# contrive a quadratic time series
from matplotlib import pyplot
series = [i**2 for i in range(1,101)]
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(series)
# histogram
pyplot.subplot(212)
pyplot.hist(series)
pyplot.show()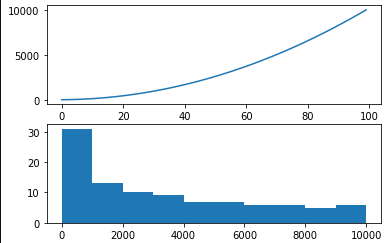
* 위의 2차 곡선을 sqrt()함수를 사용하여 제곱근을 구할 수 있다.
* 위의 예제는 완벽한 2차 곡선이므로 sqrt()를 하면 완벽한 직선 플롯이 된다.
# square root transform a contrived quadratic time series
from matplotlib import pyplot
from numpy import sqrt
series = [i**2 for i in range(1,101)]
# sqrt transform
transform = series = sqrt(series)
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(transform)
# histogram
pyplot.subplot(212)
pyplot.hist(transform)
pyplot.show()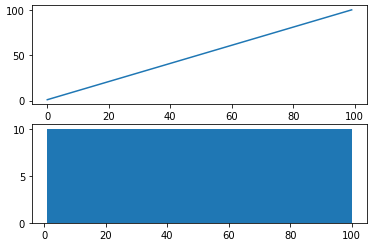
# square root transform a time series
from pandas import read_csv
from pandas import DataFrame
from numpy import sqrt
from matplotlib import pyplot
series = read_csv('airline-passengers.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
dataframe = DataFrame(series.values)
#print(dataframe)
dataframe.columns = ['passengers']
dataframe['passengers'] = sqrt(dataframe['passengers'])
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(dataframe['passengers'])
# histogram
pyplot.subplot(212)
pyplot.hist(dataframe['passengers'])
pyplot.show()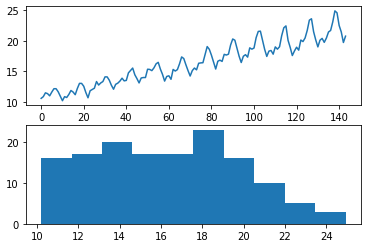
Log Transform
* 더 극단적인 trend로는 기하 급수적으로 증가,감소가 있다.
* 지수 분포가 있는 Time Series는 로그를 취해 선형으로 만들 수 있다.
* 아래는 1~100의 숫자를 지수로 사용하여 시각화한 예시이다.
# create and plot an exponential time series
from matplotlib import pyplot
from math import exp
series = [exp(i) for i in range(1,101)]
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(series)
# histogram
pyplot.subplot(212)
pyplot.hist(series)
pyplot.show()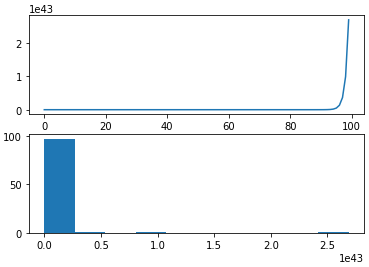
* log()함수를 사용하여 로그변환을 할 수 있다.
# log transform a contrived exponential time series
from matplotlib import pyplot
from math import exp
from numpy import log
series = [exp(i) for i in range(1,101)]
transform = log(series)
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(transform)
# histogram
pyplot.subplot(212)
pyplot.hist(transform)
pyplot.show()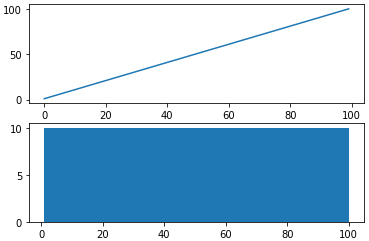
* passengers dataset을 log transform을 하면 히스토그램을 통해 더 균일하거나 축소된 가우시안과 같은 분포를 보인다
# log transform a time series
from pandas import read_csv
from pandas import DataFrame
from numpy import log
from matplotlib import pyplot
series = read_csv('airline-passengers.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
dataframe = DataFrame(series.values)
dataframe.columns = ['passengers']
dataframe['passengers'] = log(dataframe['passengers'])
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(dataframe['passengers'])
# histogram
pyplot.subplot(212)
pyplot.hist(dataframe['passengers'])
pyplot.show()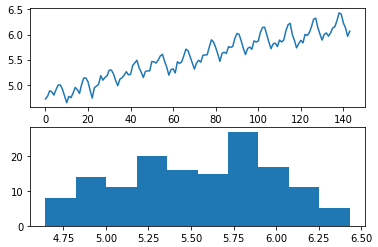
* 로그변환은 log를 사용하므로 값이 양수라고 가정을 해야된다.
Box-Cox Transform
* 제곱근 변환 및 로그 변환은 power transforms이라고 불리는 transforms class에 속한다.
* boxcox()에서 lambda에 따라 어떤 transform을 사용할 지 결정한다.
* 여러 변환을 수행할 수 있어 time series의 transform을 위한 강력한 도구로 사용할 수 있다.
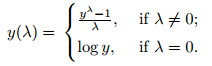

# manually box-cox transform a time series
from pandas import read_csv
from pandas import DataFrame
from scipy.stats import boxcox
from matplotlib import pyplot
series = read_csv('airline-passengers.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
dataframe = DataFrame(series.values)
dataframe.columns = ['passengers']
dataframe['passengers'] = boxcox(dataframe['passengers'], lmbda=0.0)
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(dataframe['passengers'])
# histogram
pyplot.subplot(212)
pyplot.hist(dataframe['passengers'])
pyplot.show()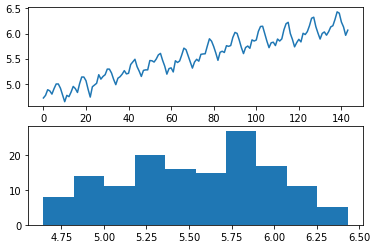
# automatically box-cox transform a time series
from pandas import read_csv
from pandas import DataFrame
from scipy.stats import boxcox
from matplotlib import pyplot
series = read_csv('airline-passengers.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
dataframe = DataFrame(series.values)
dataframe.columns = ['passengers']
dataframe['passengers'], lam = boxcox(dataframe['passengers']) # boxcox함수에서 lamda prameter를 설정하지 않으면 lamda를 제2 return한다
print('Lambda: %f' % lam)
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(dataframe['passengers'])
# histogram
pyplot.subplot(212)
pyplot.hist(dataframe['passengers'])
pyplot.show()
Lambda: 0.148023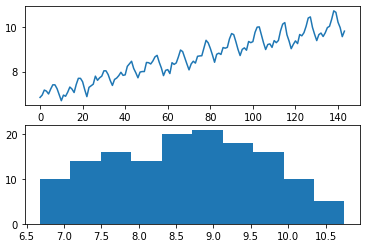
'Study > time series forecasting with python' 카테고리의 다른 글
| Chapter 10. A Gentle Introduction to White Noise (0) | 2021.07.12 |
|---|---|
| Chapter 9. Moving Average Smoothing (0) | 2021.07.12 |
| Chapter 7. 추가 내용 (0) | 2021.06.14 |
| Chapter 7. Resampling and Interpolation (0) | 2021.06.14 |
| Chapter 6. Data Visualization (0) | 2021.05.27 |
