Chapter 15에서는
* line-plot을 사용하여 stationary 및 non-stationary time series를 식별하는 방법
* 시간에 따른 변화에 대한 평균 및 분산과 같은 요약 통계를 확인하는 방법
* time series가 stationary한 지 확인하기 위해 통계적으로 유의한 테스트를 사용하는 방법에 대해 배운다.
Stationary Time Series
* stationary하다는 말은 time series가 시간에 의존하지 않는다는 말이다.
* time series가 trend, seasonal effect가 없는 경우 stationary하다.
* 아래의 예제는 일별 여성 출생수에 대한 dataset이다.
# load time series data
from pandas import read_csv
from matplotlib import pyplot
series = read_csv('./dataset/daily-total-female-births.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
series.plot()
pyplot.show()
# multiplicative decompose time series
if 1:
from matplotlib import pyplot
from statsmodels.tsa.seasonal import seasonal_decompose
series = read_csv('./dataset/daily-total-female-births.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
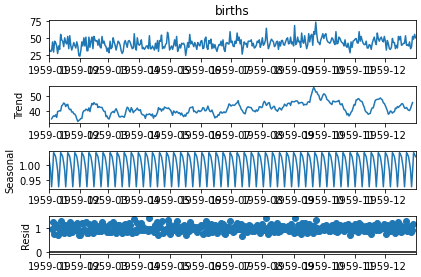
result = seasonal_decompose(series, model='multiplicative') #additive multiplicative
result.plot()
pyplot.show()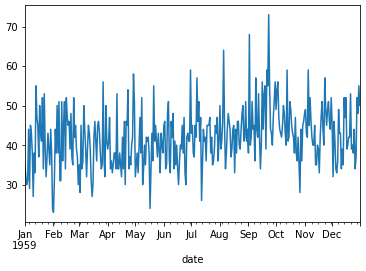
Non-stationary Time Series
* non-stationary한 time series는 trend, seasonal effect, 시간 등에 의존한다.
* 평균 및 분산과 같은 요약 통계는 시간이 지남에 따라 변경된다.
* 이는, trend와 seasonal components를 제거함에 따라 stationary하게 만들 수 있다.
# load time series data
from pandas import read_csv
from matplotlib import pyplot
series = read_csv('airline-passengers.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
series.plot()
pyplot.show()
from matplotlib import pyplot
from statsmodels.tsa.seasonal import seasonal_decompose
series = read_csv('airline-passengers.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
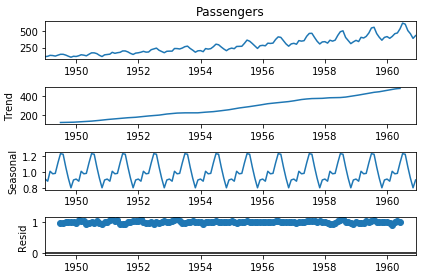
result = seasonal_decompose(series, model='multiplicative') #additive multiplicative
result.plot()
pyplot.show()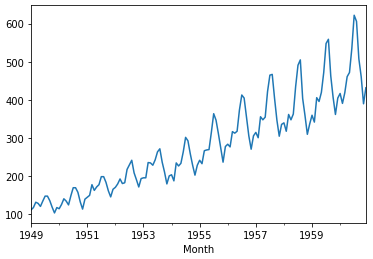
Type of Stationary Time Series
* Stationary Process : stationary한 관측치를 생성하는 process
* Stationary Model : stationary한 관측치를 설명하는 model
* Trend Stationary : trend가 없는 time series
* Seasonal Stationary : seasonailty가 없는 time series
* Stictly Stationary : stationary process의 수학적 정의, 특히 관측값의 분포가 시간에 대해 불변
Stationary Time Series and Forecasting
* trend, seasonality를 제거함으로써 stationary한 time series를 만들면,
* 예측하는데 있어서 데이터의 더 명확한 신호를 통해 이점을 얻을 수 있다.
Checks for Stationarity
* Look at Plots : 데이터를 시각화해서 stationary한 지 알 수 있다.
* Summary Statistics : 데이터에 대한 요약 통계를 냄으로써 stationary한 지 알 수 있다.
* Statistical Tests : 통계 테스트를 사용하여 stationarity에 대한 기대치를 충족했는 지 확인가능하다.
Daily Births Dataset
* Dailry Births dataset을 이용하여 시각화를 하는 것에 대해 다룬다.
* 또한, dataset을 2분할로 나누고 이에 대한 평균, 분산을 비교하는 것에 대해 다룬다.
* 관측치에 대한 분포가 가우시안을 따르고 평균과 분산이 크게 차이나지 않으므로 stationary time series라고 볼 수 있다.
# plot a histogram of a time series
from pandas import read_csv
from matplotlib import pyplot
series = read_csv('daily-total-female-births.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
series.hist()
pyplot.show()
# calculate statistics of partitioned time series data
from pandas import read_csv
series = read_csv('daily-total-female-births.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
X = series.values
split = int(len(X) / 2)
X1, X2 = X[0:split], X[split:]
mean1, mean2 = X1.mean(), X2.mean()
var1, var2 = X1.var(), X2.var()
print('mean1=%f, mean2=%f' % (mean1, mean2))
print('variance1=%f, variance2=%f' % (var1, var2))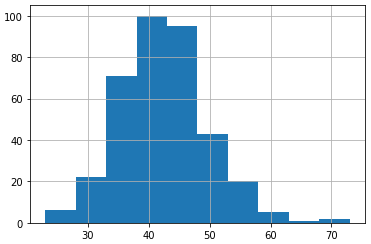
mean1=39.763736, mean2=44.185792
variance1=49.213410, variance2=48.708651
Airline Passengers Dataset
* 시간이 다른 두 집단으로 분할한다. 이에 대해 요약통계를 내는 것에 대해 다룬다.
* 이 때, 두 집단에 대한 평균과 분산이 많이 차이남을 확인할 수 있다.
* 따라서 이 dataset은 non-stationary time series라고 볼 수 있다.
* 또한 시각화했을 경우, trend가 분명히 있음을 알 수 있다.
# calculate statistics of partitioned time series data
from pandas import read_csv
series = read_csv('airline-passengers.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
X = series.values
split = int(len(X) / 2)
X1, X2 = X[0:split], X[split:]
mean1, mean2 = X1.mean(), X2.mean()
var1, var2 = X1.var(), X2.var()
print('mean1=%f, mean2=%f' % (mean1, mean2))
print('variance1=%f, variance2=%f' % (var1, var2))
# plot a histogram of a time series
from pandas import read_csv
from matplotlib import pyplot
series = read_csv('airline-passengers.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
series.hist()
pyplot.show()
mean1=182.902778, mean2=377.694444
variance1=2244.087770, variance2=7367.962191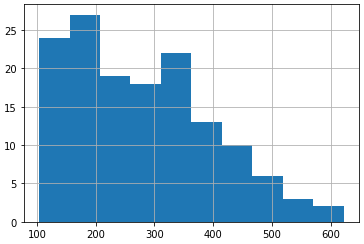
* 일단 dataset plot을 보면, 지수함수와 같은 trend를 가짐을 알 수 있다. 주기도 있음을 알 수 있다.
* 이는 로그함수를 사용하여 선형 변환이 가능하다.
* 로그함수를 사용하면 가우스 분포와 유사하게 변형됨을 알 수 있다.
* 하지만 아직은 trend와 주기(계절적 요소)가 있는 것을 볼 수 있다.
# histogram and line plot of log transformed time series
from pandas import read_csv
from matplotlib import pyplot
from numpy import log
series = read_csv('airline-passengers.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
X = series.values
pyplot.plot(X)
pyplot.show()
X = log(X)
pyplot.hist(X)
pyplot.show()
pyplot.plot(X)
pyplot.show()
from matplotlib import pyplot
from statsmodels.tsa.seasonal import seasonal_decompose
result = seasonal_decompose(series, model='multiplicative', period=1)
result.plot()
pyplot.show()
result = seasonal_decompose(X, model='multiplicative', period=1) #additive multiplicative
result.plot()
pyplot.show()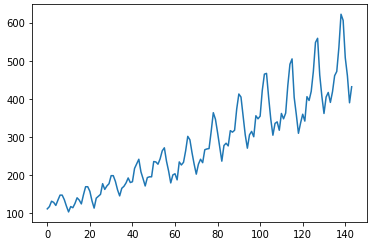
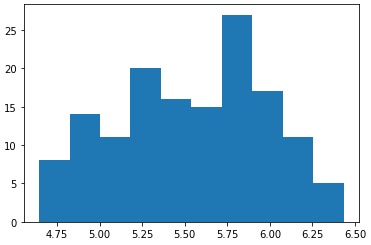
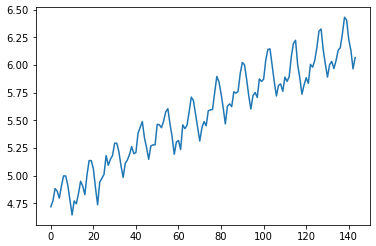
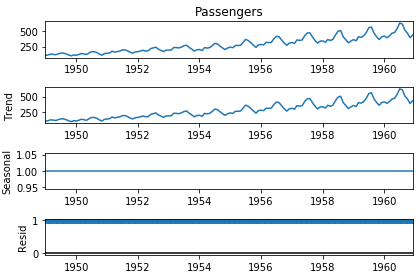
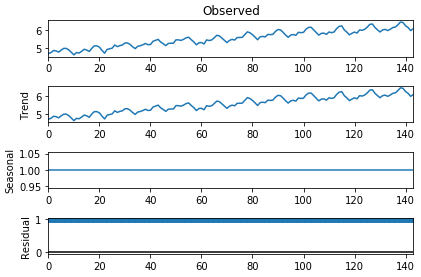
* 앞의 dataset을 로그변환후 요약통계를 내는 예제이다.
* 평균과 분산이 비슷하지만, line-plot을 검토했을 때는 stationary하지 않다고 생각할 수 있다.
* 즉, 요약 통계는 그렇게 정확한 지표는 아니다.
* 그래서 요약 통계 대신 통계 테스트를 사용해야한다.
# calculate statistics of partitioned log transformed time series data
from pandas import read_csv
from numpy import log
series = read_csv('airline-passengers.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
X = series.values
X = log(X)
split = int(len(X) / 2)
X1, X2 = X[0:split], X[split:]
mean1, mean2 = X1.mean(), X2.mean()
var1, var2 = X1.var(), X2.var()
print('mean1=%f, mean2=%f' % (mean1, mean2))
print('variance1=%f, variance2=%f' % (var1, var2))
mean1=5.175146, mean2=5.909206
variance1=0.068375, variance2=0.049264
Augmented Dickey-Fuller test
* ADF는 dataset에 대해 하나의 가정을 하고, 그 가정이 참일 확률에 대해 알려주는 통계 테스트이다.
* ADF를 이용하면 Time series가 stationary한 지 non-stationary한 지 확인할 수 있다.
* Null Hypothesis(H0) 귀무가설 : Time Series에 단위근이 있음을 나타내며 이 말은 non-stationary하다. 즉, 시간에 의존적이다 라는 의미를 지닌다.
* Alternate Hypothesis(H1) 대립가설 : 귀무 가설이 기각된다. 이는 단위근이 없음을 나타내며 stationary하다 -> 시간에 의존적이지 않다 라는 의미를 지닌다.
* 위의 두 가지는 p-value를 사용하여 해석한다.
* 만약 p-value>0.05이면 H0, p-value<=0.05이면 H1의 의미를 지닌다.
* 예제를 실행하면 ADF값은 -4.8로 나온다. 이 값은 낮을 수록 P값이 0.05보다 작을 확률이 높다.
* 또한 ADF값이 1%의 임계값보다 작음을 알 수 있다. 이는 1% 미만의 유의수준(우연일 확룰)이 있다는 것을 나타낸다.
# calculate stationarity test of time series data
from pandas import read_csv
from statsmodels.tsa.stattools import adfuller
series = read_csv('daily-total-female-births.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
X = series.values
result = adfuller(X)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
print('\t%s: %.3f' % (key, value))
ADF Statistic: -4.808291
p-value: 0.000052
Critical Values:
1%: -3.449
5%: -2.870
10%: -2.571* 다음으로는 AIRLINE-PASSENGERS DATASET에 대한 검증이다.
* 위에서 이 DATASET은 non-stationary -> 시간에 의존하는 dataset임을 알고 있다.
* 통계를 내리면 그에 대해 일치하는 결과를 보인다.
* 또한, log변환을 통해 그나마 시간 의존도를 낮추면 p값과 ADF값이 낮아짐을 알 수 있다.
# calculate stationarity test of time series data
from pandas import read_csv
from statsmodels.tsa.stattools import adfuller
series = read_csv('airline-passengers.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
X = series.values
result = adfuller(X)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
print('\t%s: %.3f' % (key, value))
ADF Statistic: 0.815369
p-value: 0.991880
Critical Values:
1%: -3.482
5%: -2.884
10%: -2.579
# calculate stationarity test of log transformed time series data
from pandas import read_csv
from statsmodels.tsa.stattools import adfuller
from numpy import log
series = read_csv('airline-passengers.csv', header=0, index_col=0, parse_dates=True,
squeeze=True)
X = series.values
X = log(X)
result = adfuller(X)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
for key, value in result[4].items():
print('\t%s: %.3f' % (key, value))
ADF Statistic: -1.717017
p-value: 0.422367
1%: -3.482
5%: -2.884
10%: -2.579'Study > time series forecasting with python' 카테고리의 다른 글
| Chapter 17. Forecasting Performance Measures (0) | 2021.07.21 |
|---|---|
| Chapter 16. Backtest Forecast Model (0) | 2021.07.21 |
| Chapter 14. Use and Remove Seasonality (0) | 2021.07.21 |
| Chapter 13. Use and Remove Trends (0) | 2021.07.21 |
| Chapter 12. Decompose Time Series Data (0) | 2021.07.12 |
